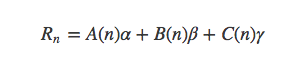汉诺塔问题

3个柱子的汉诺塔问题，最少移动次数记为T(n)。
T(n)=2T(n−1)+1
边界条件为T(0)=0。解出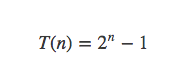

其中等比数列求和公式为：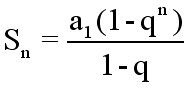

递归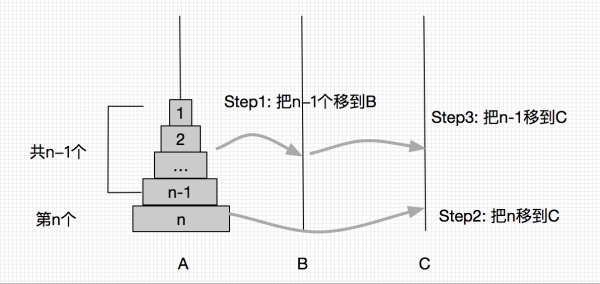

移动的时候的原则就如下表示：
第一阶段：（n-1）A—>B（把所有的n-1个盘子从A移动到B上）
第二阶段：n A—>C（把最底下的n号盘从A移动到C上）
第三阶段：（n-1）B—>C（把n-1个盘子从B移动到C上）

直线分割平面问题

n条直线最多分割平面为几部分，记为L(n)。所以。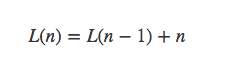

边界条件为L(0)=1。得。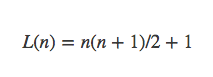

这题有个扩展，n个V型最多分割平面为几部分？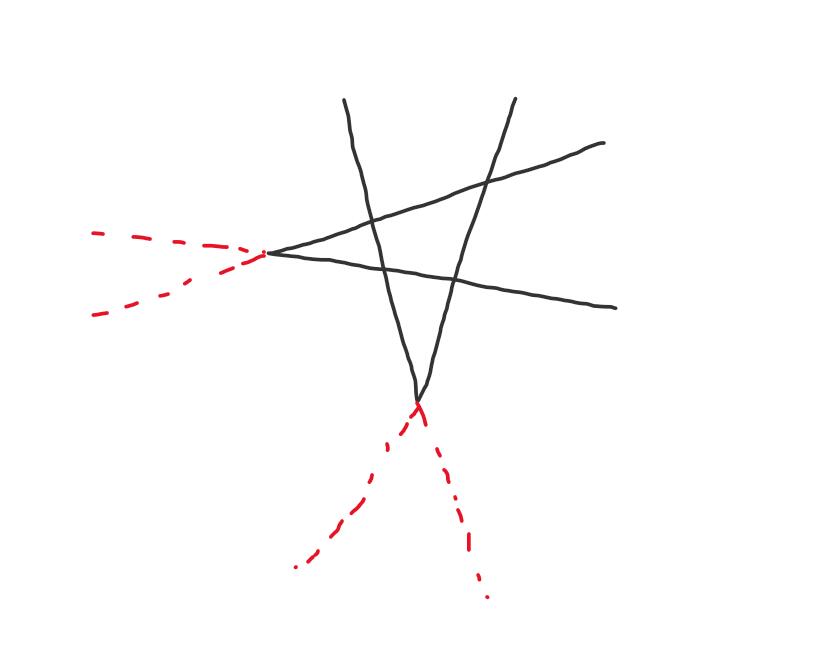

将V型补全（红色虚线部分），那么就转化为了2n条直线划分平面数，那么n个V型划分数只要减去2n就行了，所以答案为：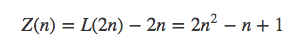

约瑟夫环问题

约瑟夫问题是个有名的问题：N个人围成一圈，从第一个开始报数，第M个将被杀掉，最后剩下一个，其余人都将被杀掉。例如N=6，M=5，被杀掉的顺序是：5，4，6，2，3，1。
书中的例子是每隔一个人杀死一个。J（n）是最后一个幸存者的位置。

分两种情况讨论：
当有2n个人时，踢掉n个人之后，情况如下图所示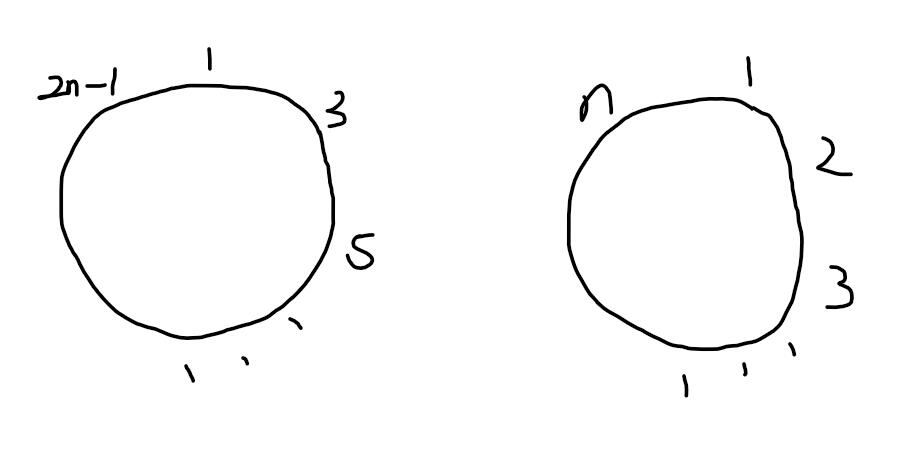

观察发现一圈当中的对应位置相同，且左图的数字为右图数字*2-1。所以最后幸存者的位置也有着相同的关系。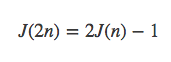

同理，当有2n+1个人时，踢掉n+1个人之后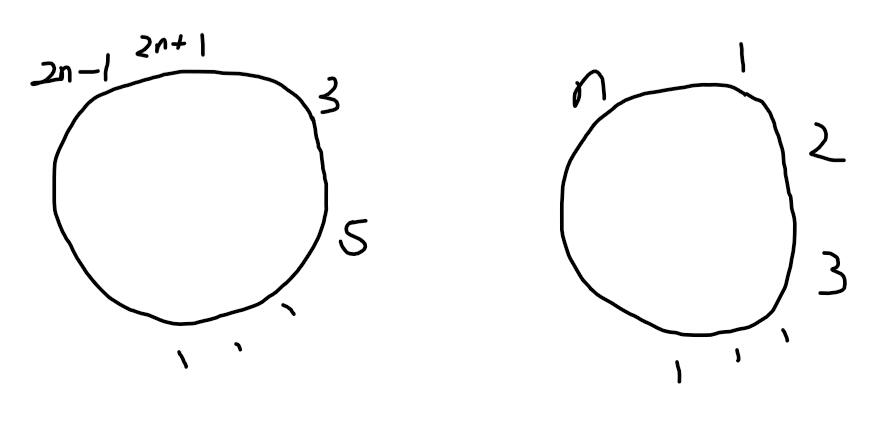

观察对应关系可以得出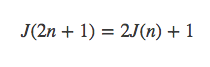

边界条件为，J(1)=1。
这个递推式很难求解，但是枚举出前面几项可以发现，如果令n=2的m次方+l，其中2的m次方是小于等于n的最大2的幂，那么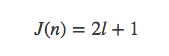

将n写成二进制可以发现，f(n)就是n的二进制循环左移1位。如n=10，即1010，f(10)=0101=5。
现在将其推广到一般形式，原始的式子中α=1，β=-1，r=1。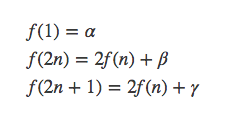

由此可见可以设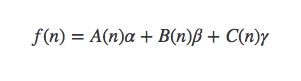

令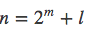

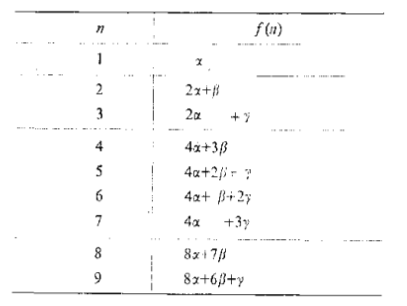
通过观察得出：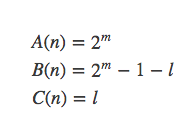

将递推式继续推广：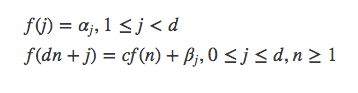

可以得到解为：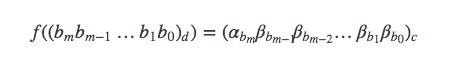

具体为：

递推式求和

使用成套方法。
成套方法的一般步骤是：寻求一组已知其解的通用参数，然后将特殊情况组合起来得到一般的情形，
有多少个独立的参数就需要多少个独立的特解。
求解如下递推式：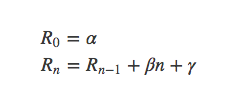

用成套方法求解，设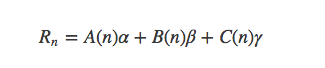

对于更复杂得递推式：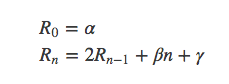

同样设